本篇文章为大家介绍了如何利用Axure打造“指示线跟随地图所选区域,并展示相应数据可视化”的效果,其中需要做到的函数计算为重难点。
知识重点难点
- 直角三角形斜边长度与斜边角度计算;
- 进度条制作。
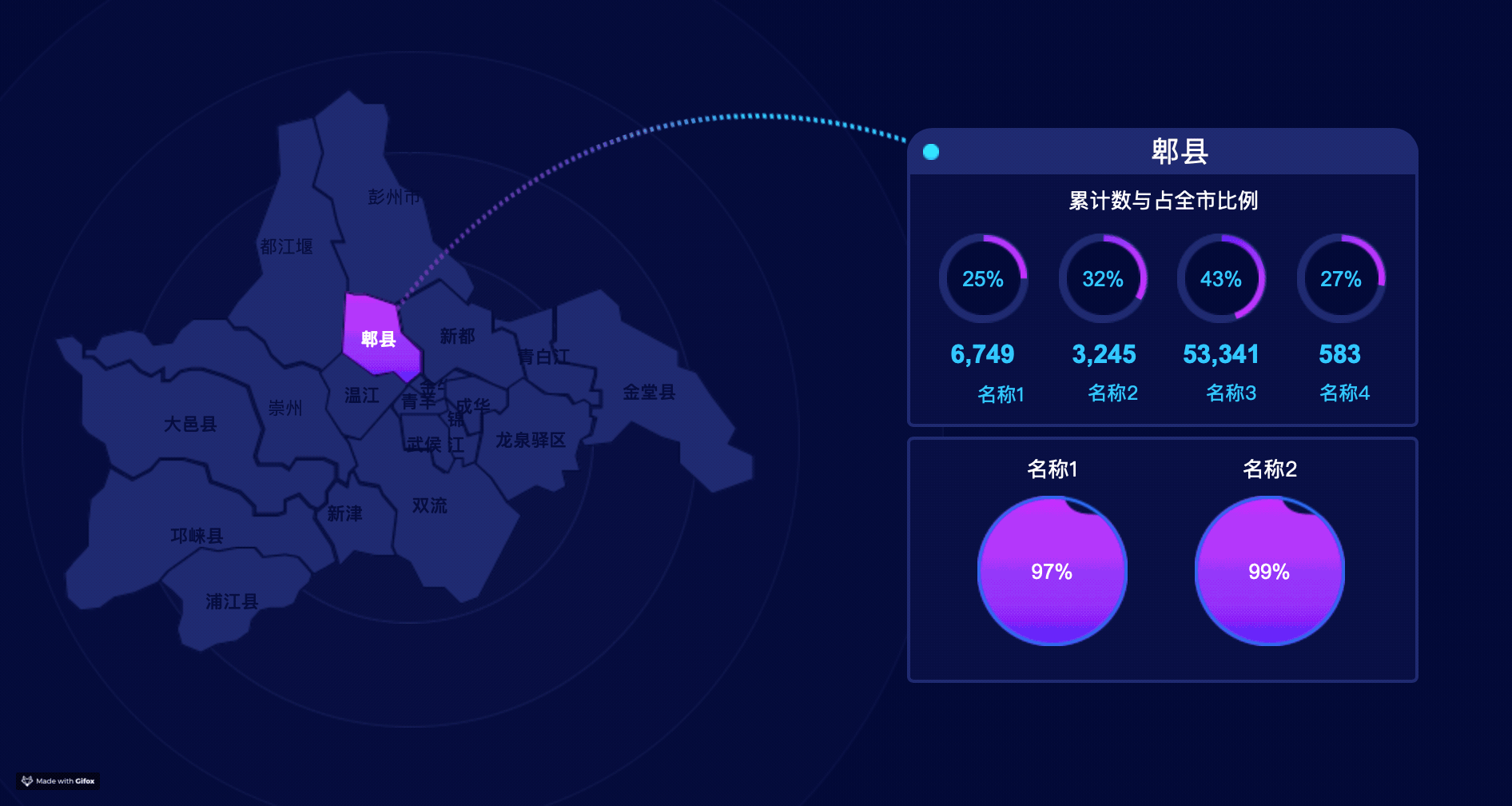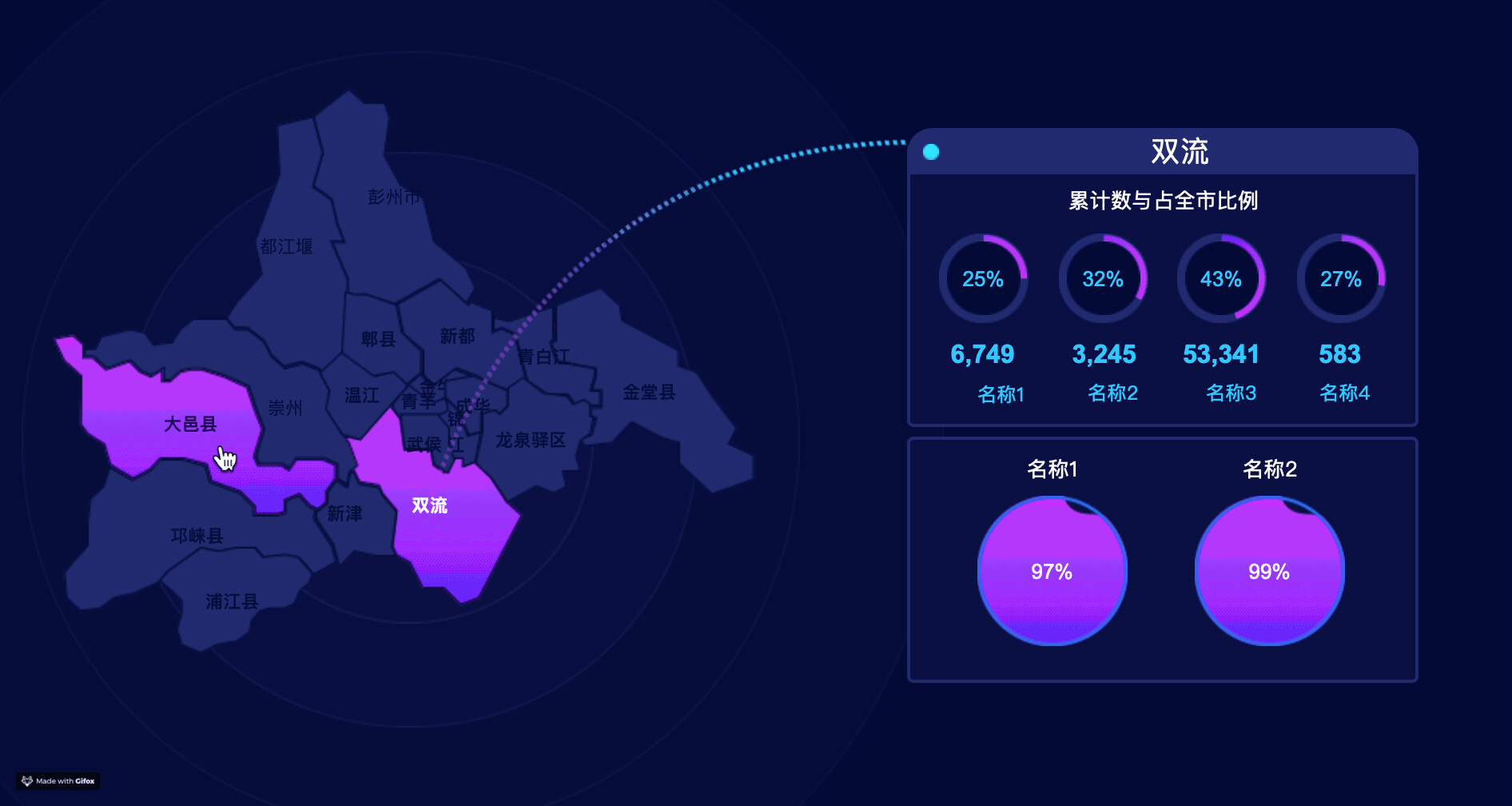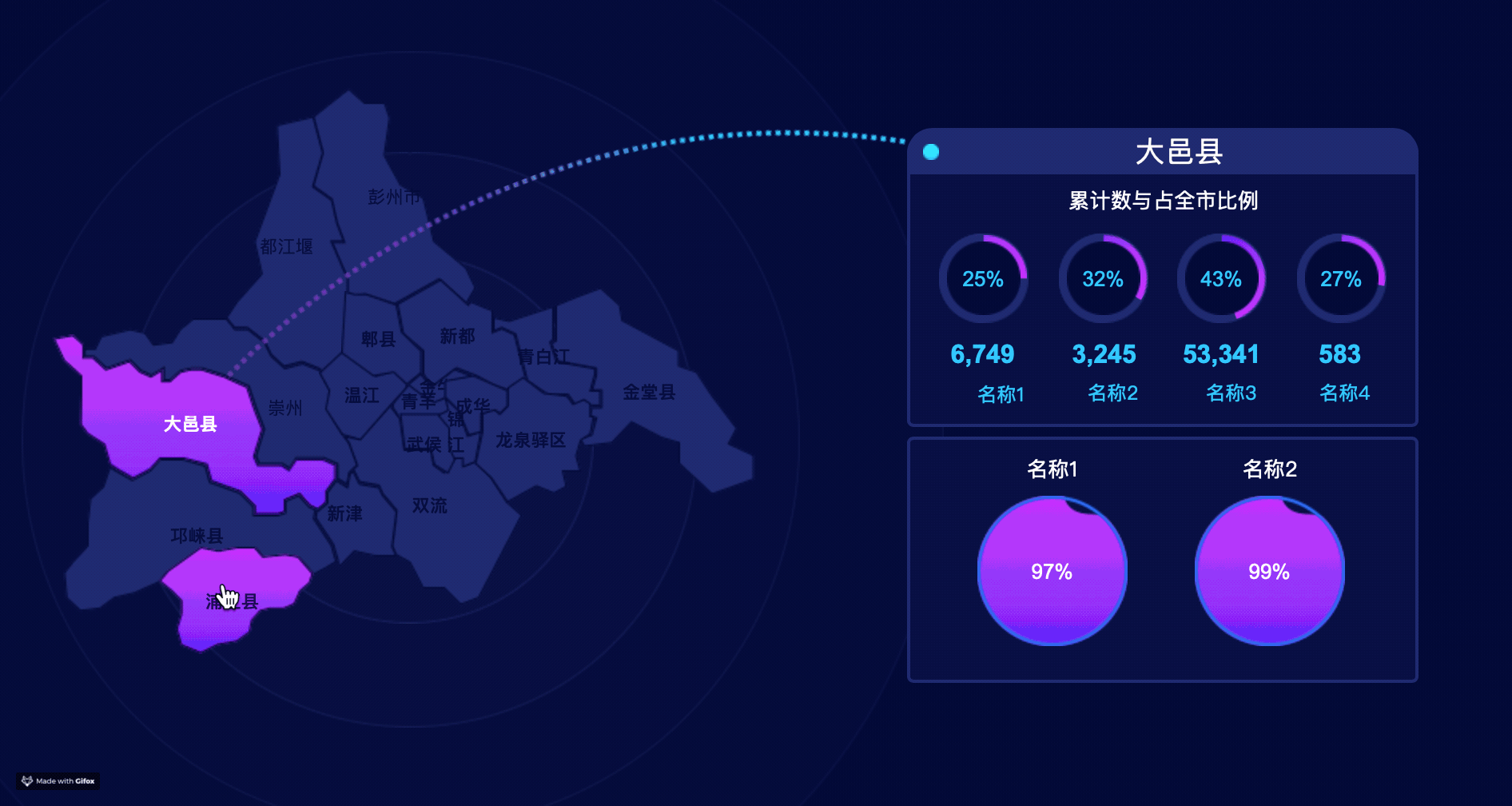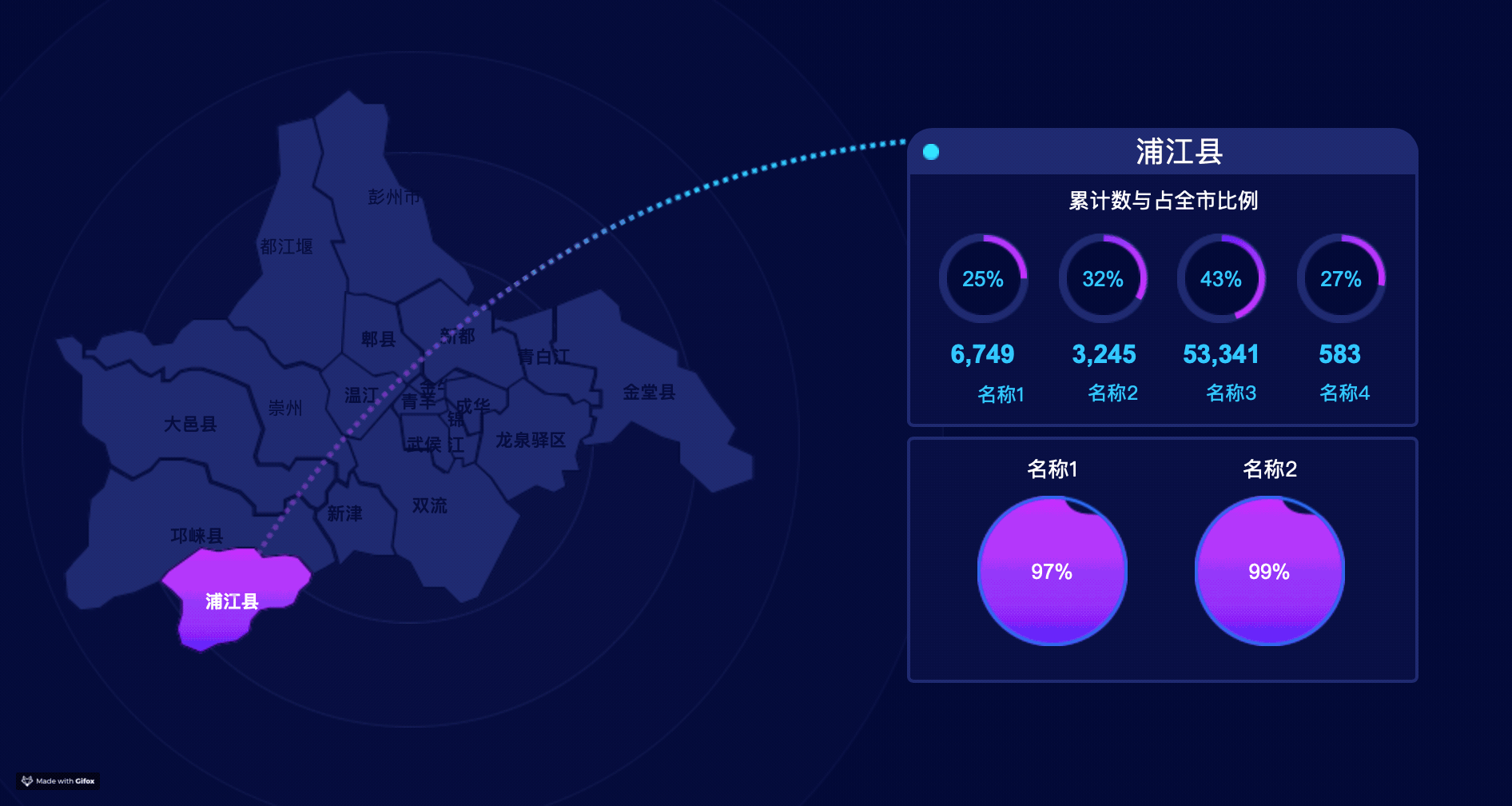
元件准备
地图“map”
- 钢笔勾出地图各板块形状,并分别命名;
- 为各形状设置Interaction Styles,主要是MouserOver与Selected;
- 选择所有形状Selection Group。
跟随线“map-line”
- 钢笔勾出一条曲线,命名为“map-line”,确保其起点与终点水平;
- 添加一个小小的圆形,命名为“P”,放置与曲线终点处。

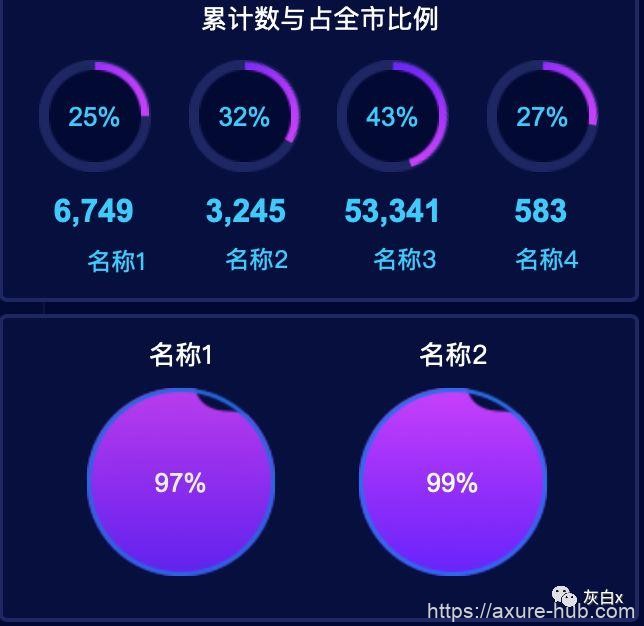
动态面板“可视化数据面板”
- 添加一动态面板命名“可视化数据面板”,配置两个状态“1”、“0”,初始状态为1;
- 状态 1 中添加数据完成时的样式内容;
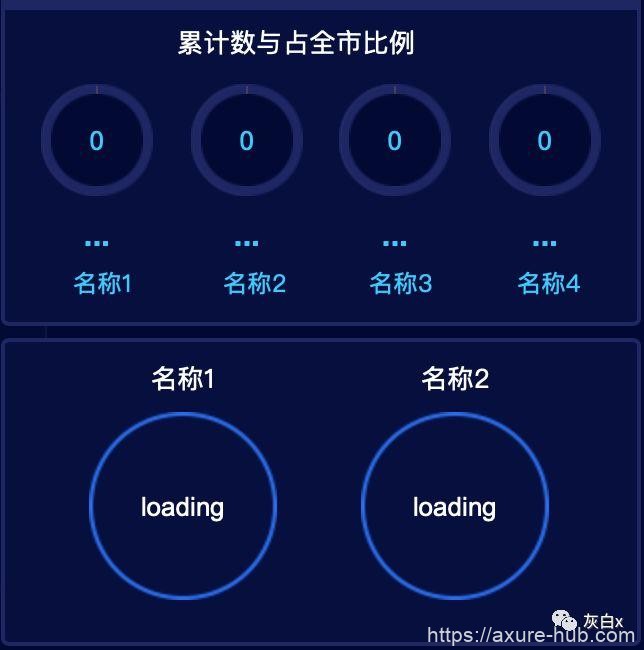
- 状态 0 中添加数据加载过程中的样式内容。
比例进度条“可视化x”
这里做的是小于50%的比例样式,添加圆或扇形如下图,每个“可视化x”均为一个动态面板,初始隐藏状态。
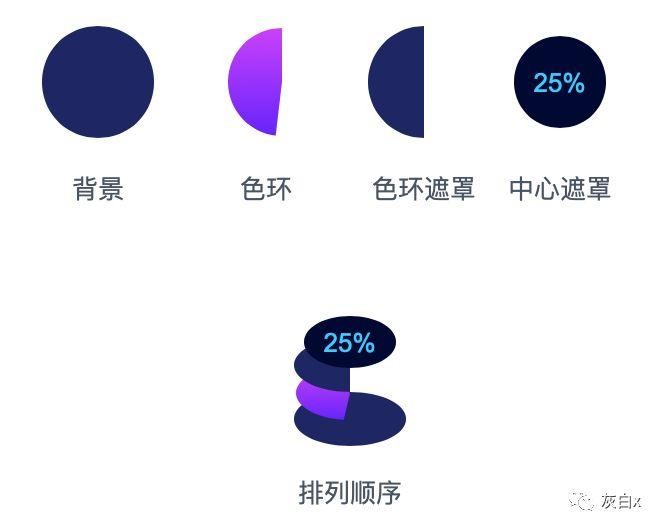
看到结构就应该知道,其实就是角度改变的做法,后面我就不详细讲了。
效果实现
主要事件与逻辑关系
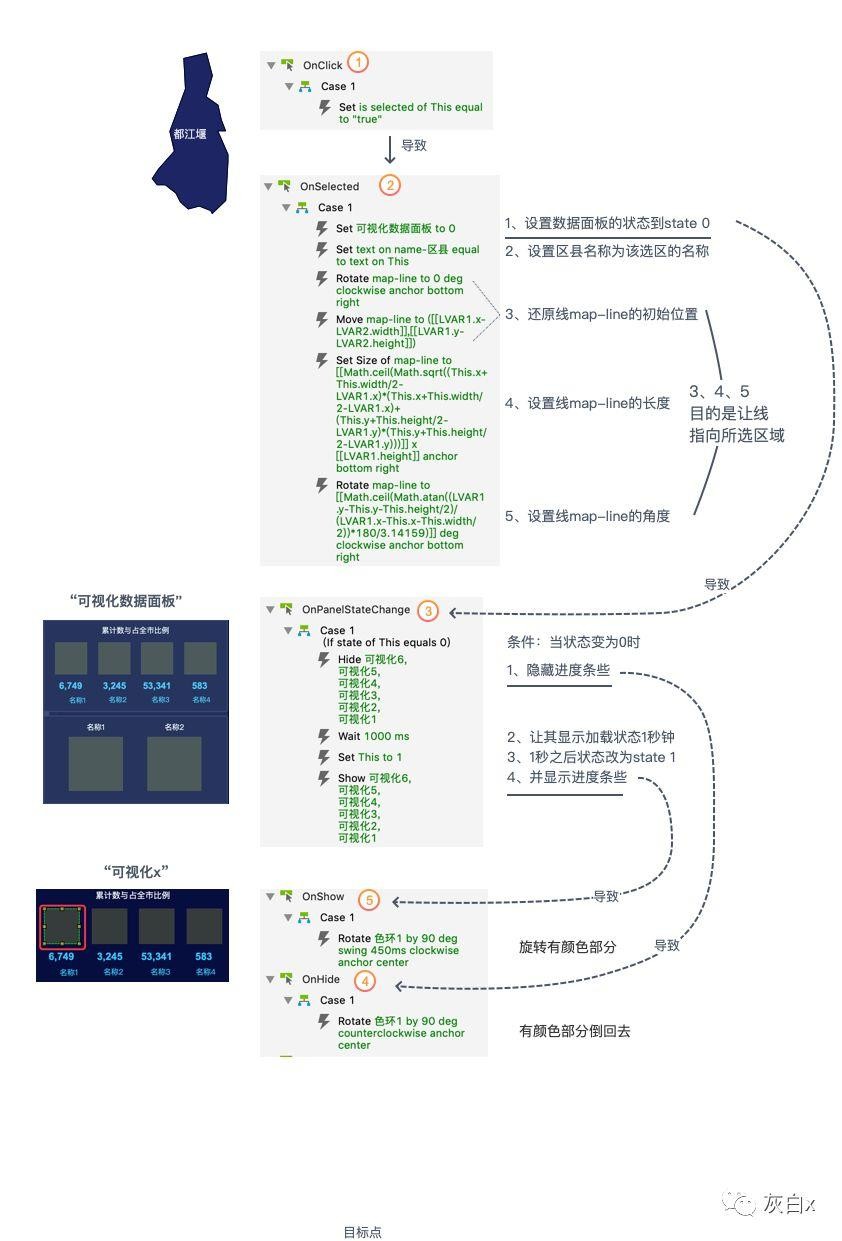
实现难点:跟随线指向所选点。
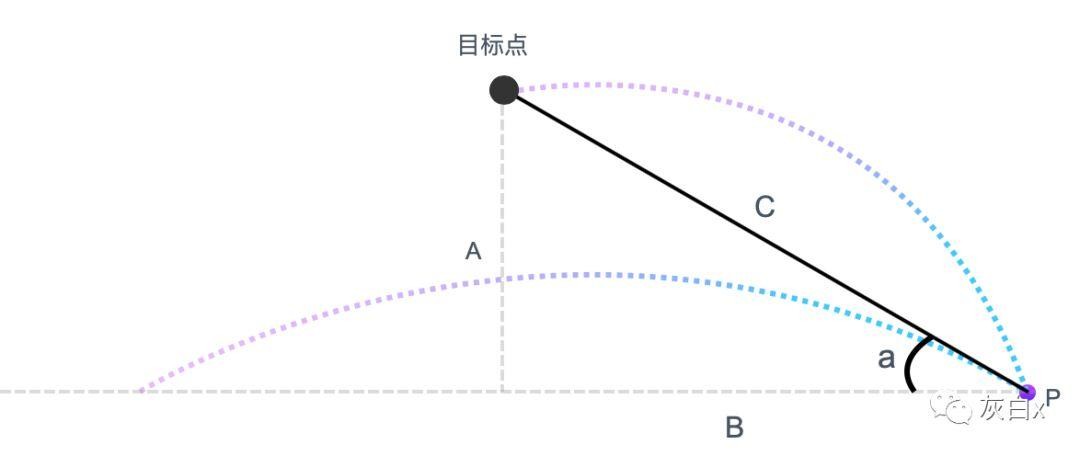
由图可知,通过得到跟随线map-line的长度C与角度a即可,又由图可知其实是求一个直角三角形的斜边长度与角度,根据数学公式最终得出如下函数计算:
C=Math.sqrt(A*A+B*B)
a=Math.atan(A/B)*180/3.14159
取整:
C=Math.ceil(Math.sqrt(A*A+B*B))
a=Math.ceil(Math.atan(A/B)*180/3.14159)
其中A、B为目标点与P点的坐标之差。
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。
